Fundamental Theorems

Gradient Theorem

Green's Theorem

Stoke's Theorem

Divergence Theorem or Gauss Theorem

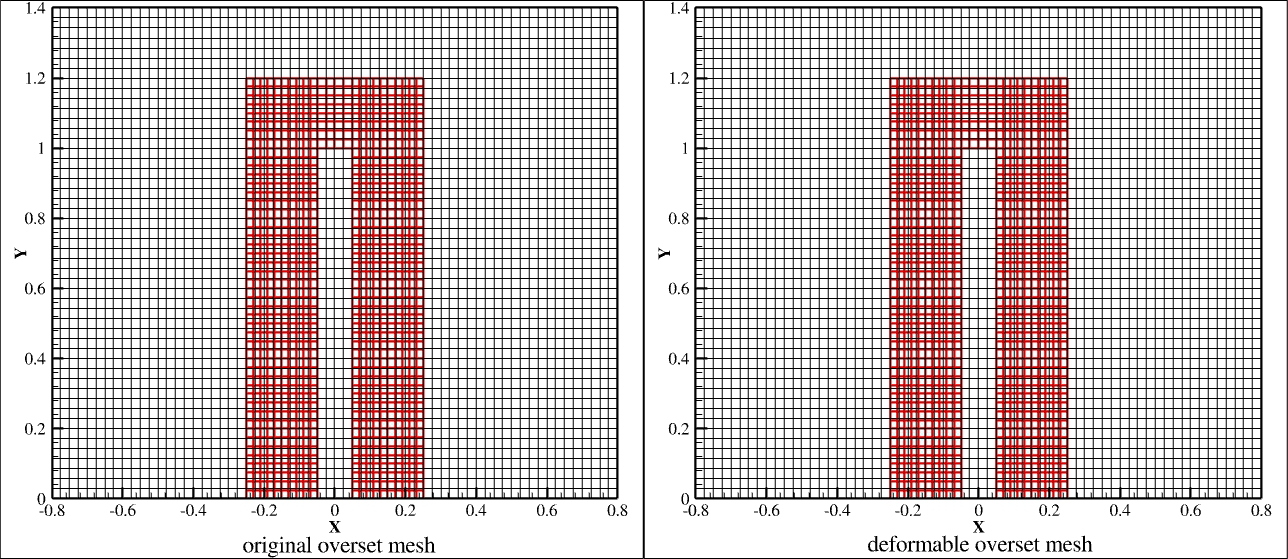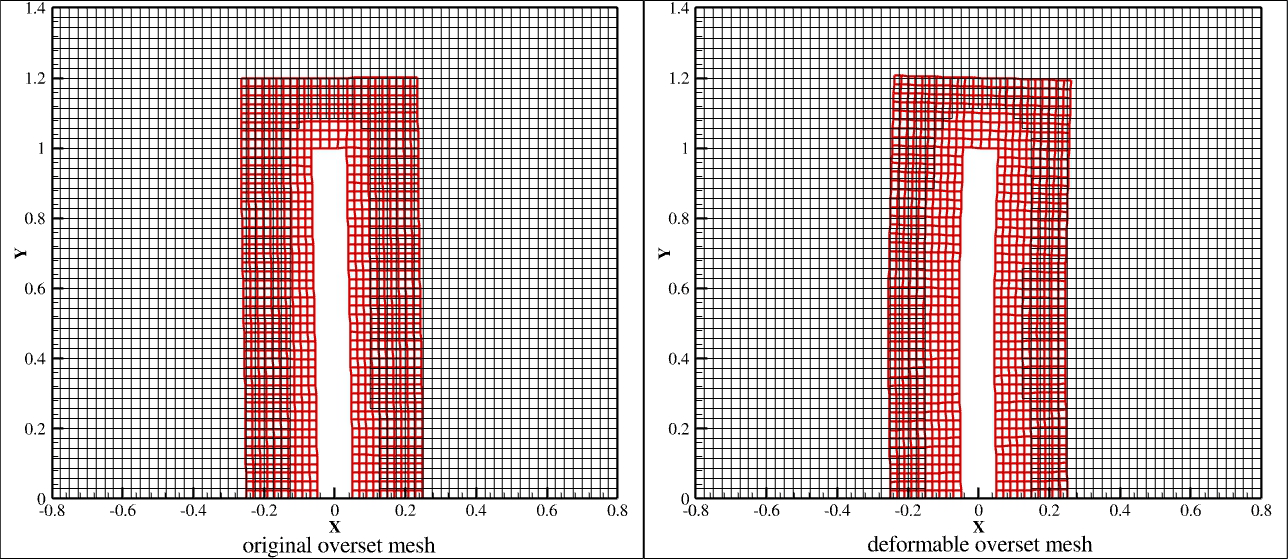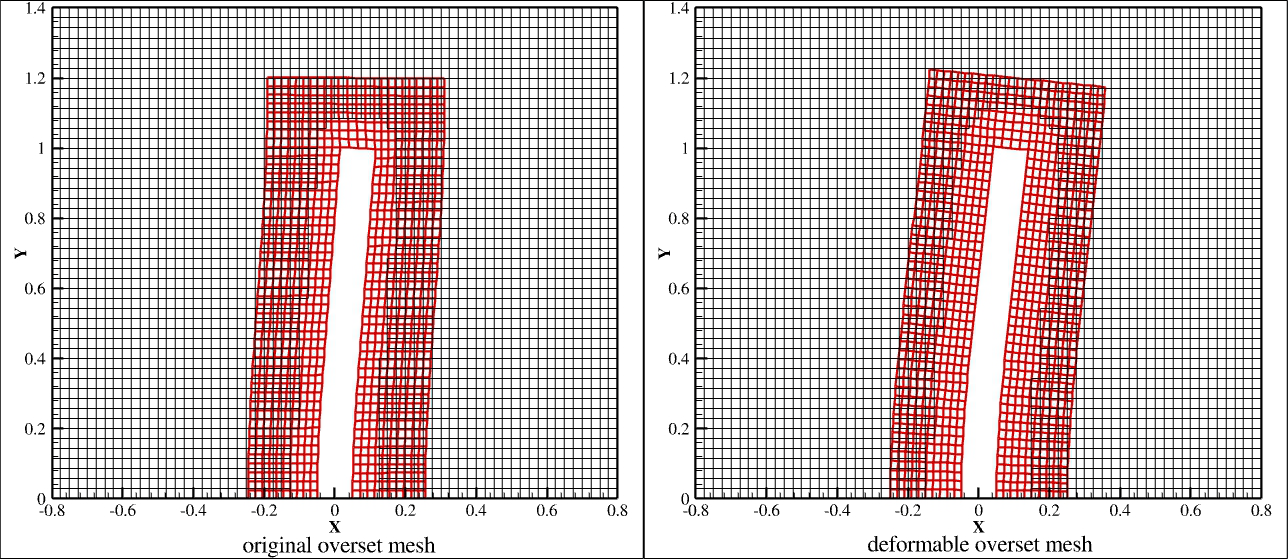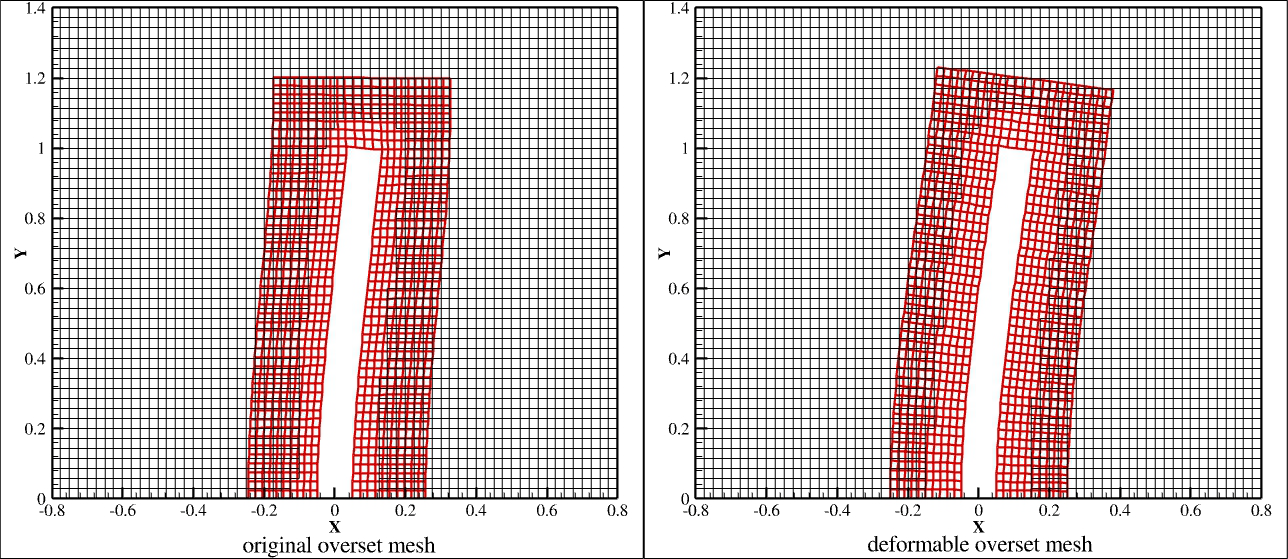
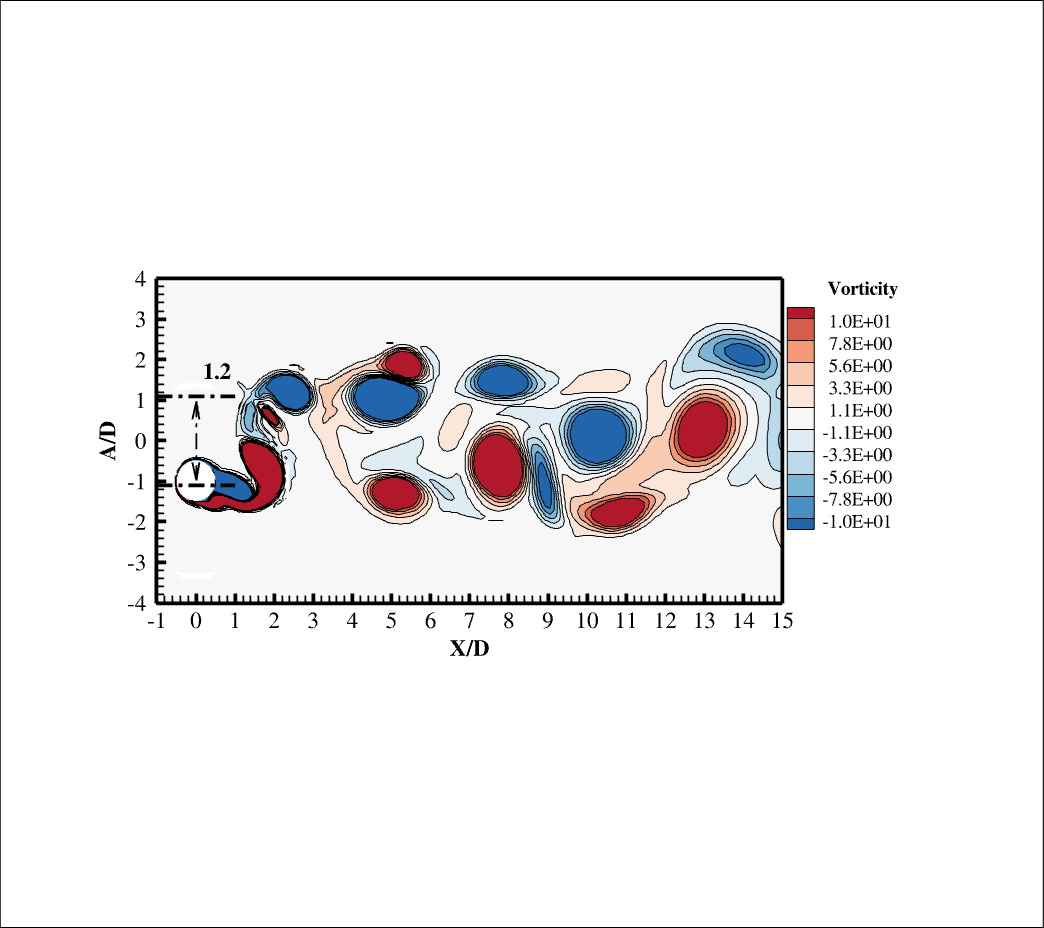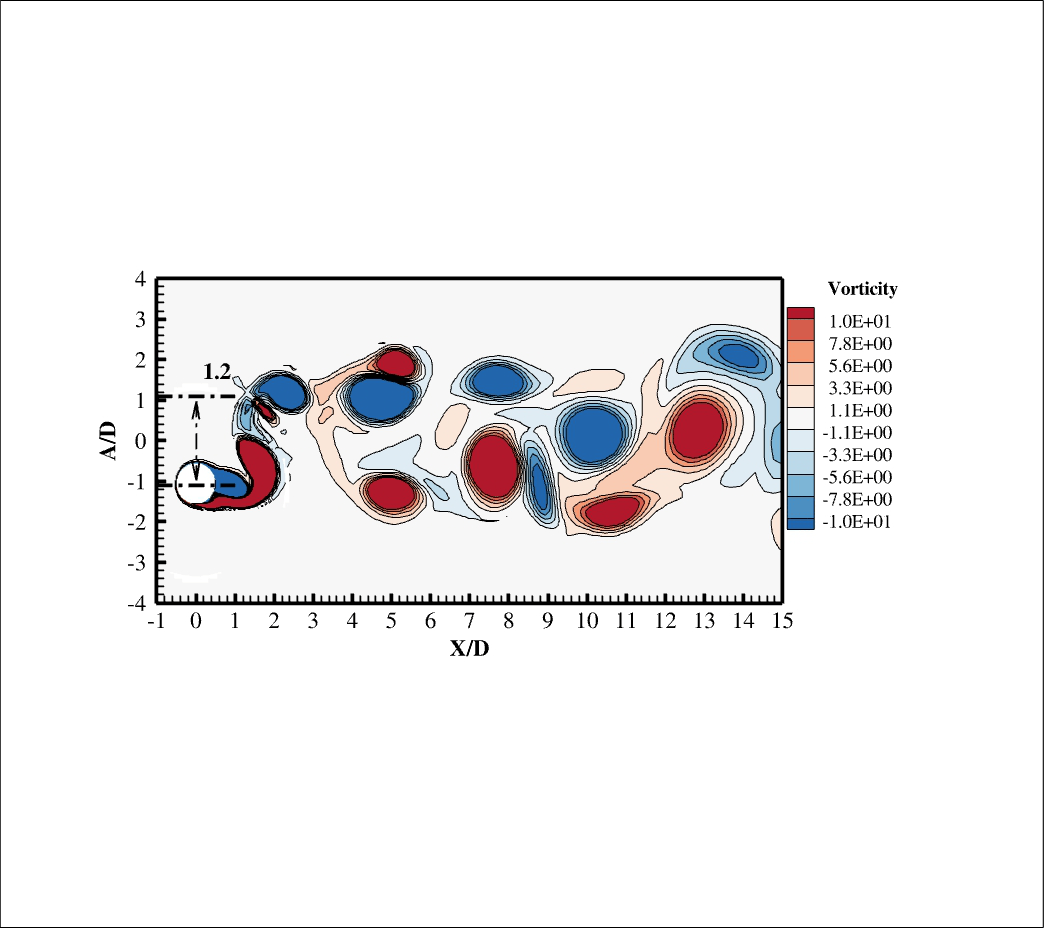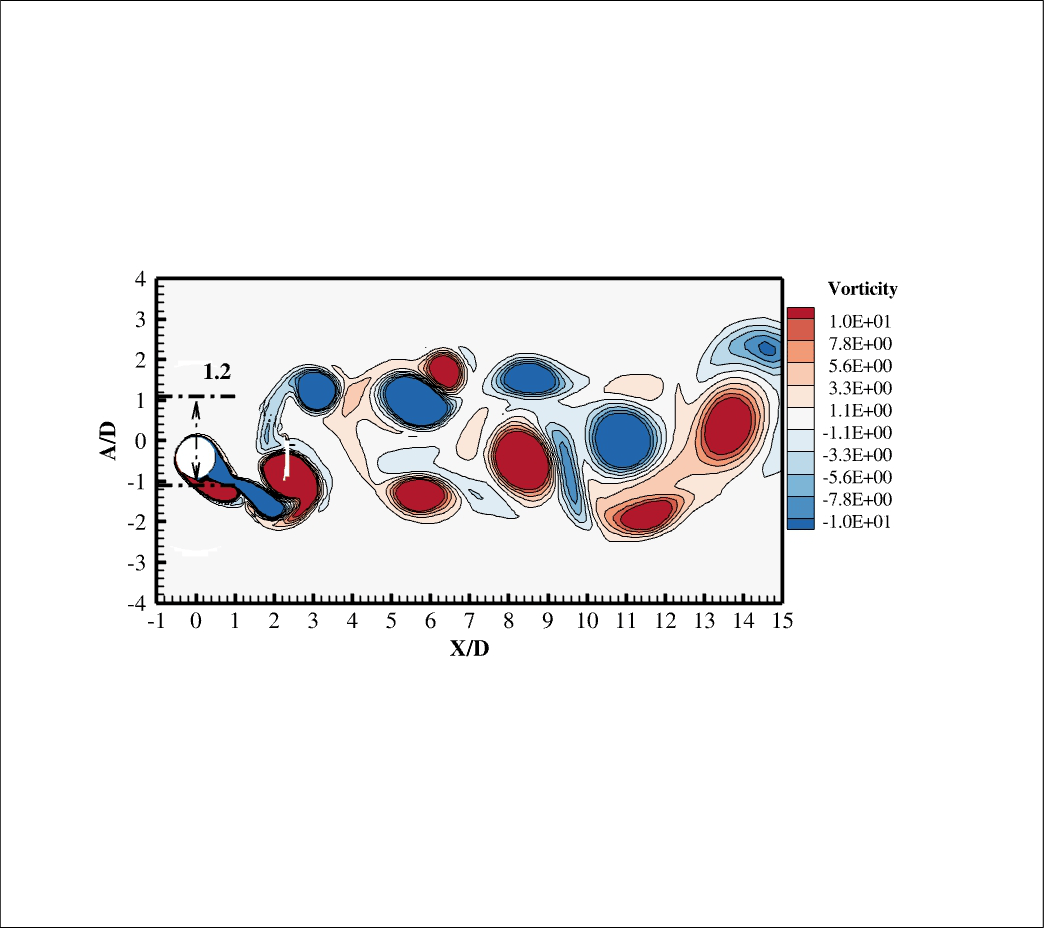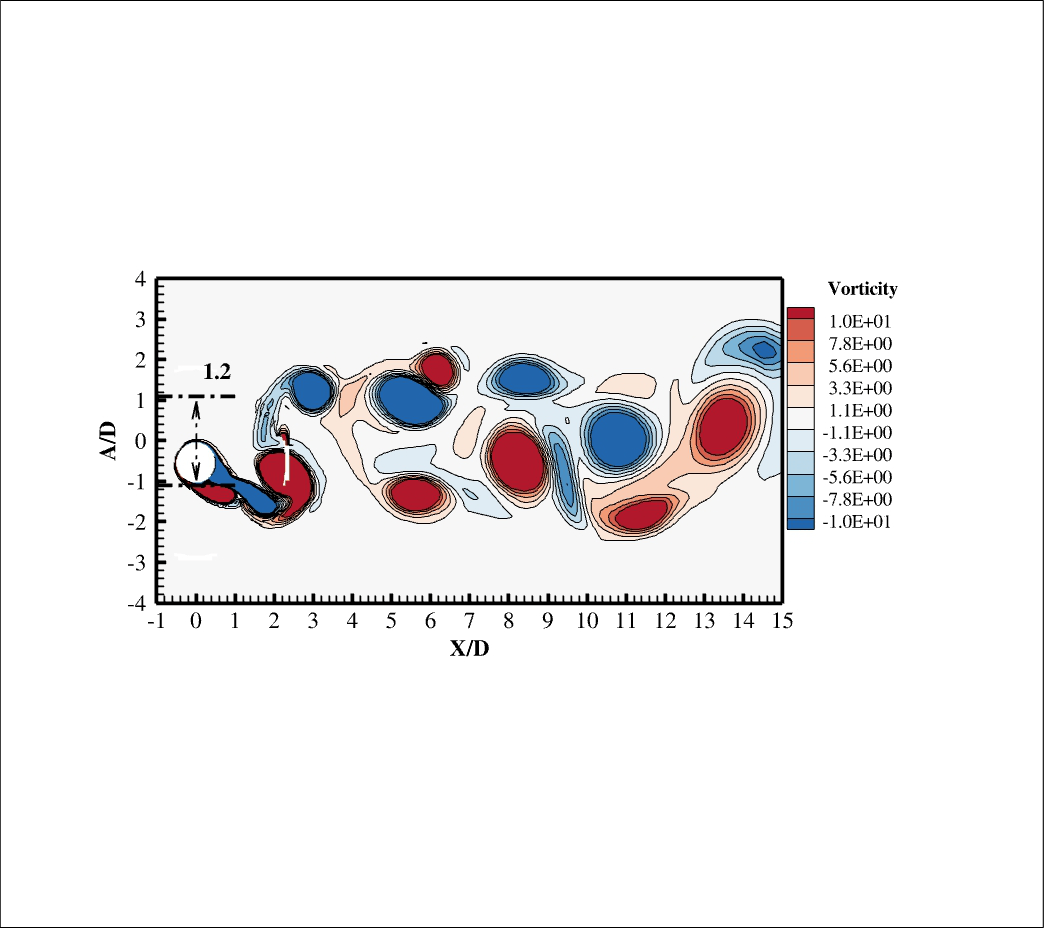
• In order to transform an equation from the differential to the integral form (vice versa), the Gauss Theorem should be applied.It's important for fluid dynamics.

• \(\boldsymbol{V}\) represents a volume in three-dimensional space of boundary \(\boldsymbol{S}\), \(\mathbf{n}\) is the outward pointing unit vector normal to \(\boldsymbol{S}\). If \(\mathbf{v}\) is a vector field defined on \(\boldsymbol{V}\), then the divergence theorem states that

\[ \oint_{\boldsymbol{S}} \mathbf{v} \bullet \mathbf{n} \mathrm{d} S=\int_{\boldsymbol{V}}(\nabla \bullet \mathbf{v}) \mathrm{d} V \]

• Implying that the net flux of a vector field through a closed surface is equal to the total volume of all sources and sinks (i.e., the volume integral of its divergence) over the region inside the surface.

Reynolds Transport Theorem

Basic Mathematics

Einsteins Summation Convention (爱因斯坦求和约定)

For vector and tensor equations, the longest but clearest notation is the Cartesian one. If the equation contains several similar terms which can be summed up , this notation can be abbreviated by applying the Einsteins summation convention.

对于向量和张量方程，最清晰且最长的表示方法就是笛卡尔表示。但是，如果这些方程中的某些项重复出现，则可以用Einsteins Summation Convention 来简化方程。

• Cartesian form

  • The Cartesian form is given by: \[ \frac{\partial \phi_x}{\partial x} + \frac{\partial \phi_y}{\partial y} +\frac{\partial \phi_z}{\partial z} \]

    To simply this equation, the Einsteins summation convention can be applied. Commonly, the summation sign \(\sum\) can be neglected to keep things clear:

    \[ \sum_{i=1} \frac{\partial \phi_i}{\partial x_i} = \frac{\partial\phi_i}{\partial x_i} , i = x,y,z \]

    For example: \[\sum_{i=1}^3 u_i u_i = u_i u_i = u_1u_1 + u_2u_2 + u_3u_3\]

• The rules of Einsteins Summation Convention

  • If the subscript appears more than once in the same term, that means summation operation, and these subscripts are called dummy index

    凡是下脚标重复出现的变量，则认定是求和运算，此时的下脚标被称为“哑标(dummy index)”

    • the dot production of two vectors 两个速度向量相乘 \[ u_i u_i = u_1u_1 + u_2u_2 + u_3u_3 \]

    • the derivative of velocity 对于速度向量求导 \[ \frac{d u_i}{d x_i} = \frac{u_1}{x_1} + \frac{u_2}{x_2} + \frac{u_3}{x_3} \]

  • If there are two different subscript in one term, for the term which repeat appears, means summation operation, while for the subscript which appears once, traverse is performed for every axis.

    如果一项中出现两个不同的脚标，对于重复出现的脚标做求和运算，对于单独出现的脚标不作求和运算，而是遍历每一个坐标轴，且每次只遍历一个，单独出现的脚标是自由自在的，称为自由标(free index)“”

    • Exp1 例子1 \[ u_j \frac{d u_i}{d x_i} = u_j \frac{d u_1}{d x_1} + u_j \frac{d u_2}{d x_2} + u_j \frac{d u_3}{d x_3} , (j = 1,2,3) \]

    • Exp2 例子2 \[ u_j \frac{d u_i}{d x_j} = u_1 \frac{d u_i}{d x_1} + u_2 \frac{d u_i}{d x_2} + u_3 \frac{d u_i}{x_3}, (i = 1,2,3) \]

  • 以N-S方程为例 Taking N-S equation for an example $$ \begin{cases} + u + v + w = f_x - + ( + + ) \

    + u + v + w = f_y - + ( + + ) \

    + u + v + w = f_z - + ( + + ) \end{cases} $$

    Every equations contain \(x,y,z\) and \(u,v,w\), they are kind of notations and can be replaced by any other symbols. For example, \(x_1, x_2, x_3\) and \(u_1, u_2, u_3\) can be used to replace \(x,y,z\) and \(u,v,w\) respectively.

    Based on the discussion above, the N-S equation can be re-written in tensor form:

    \[ \frac{\partial u_i}{\partial t} + u_j \frac{\partial u_i}{\partial x_j} = f_i - \frac{1}{\rho} \frac{\partial p}{\partial x_i} + \frac{\mu}{\rho} \frac{\partial^2 u_i}{\partial x^2_j} \]

The classification of concept -- dot product, inner product, outer product, cross product

• vector \(\mathbf{a}\) and \(\mathbf{b}\) \[ \boldsymbol{a}=\left(\begin{array}{l} a_x \\ a_y \\ a_z \end{array}\right)=\left(\begin{array}{l} a_1 \\ a_2 \\ a_3 \end{array}\right), \quad \mathbf{b}=\left(\begin{array}{l} b_x \\ b_y \\ b_z \end{array}\right)=\left(\begin{array}{l} b_1 \\ b_2 \\ b_3 \end{array}\right) \]

• tensor \(\mathbf{T}\) \[ \mathbf{T} = \left( \begin{array}{cccc} T_{11} & & T_{12} & & T_{13} \\ T_{21} & & T_{22} & & T_{23} \\ T_{31} & & T_{32} & & T_{33} \end{array} \right) \]

• Inner product or Dot product 内积 点积

  In general， for engineering, inner and dot product can be treated the same operation

  工科范围内，通常不怎么区分内积和点积

  • The inner product of two vectors \(\mathbf{a}\) and \(\mathbf{b}\) produces a scalar \(\phi\) and is commutative. This operation is indicated by the dot sign \(\bullet\)

    \[ \phi = \mathbf{a} \cdotp \mathbf{b} = \mathbf{a}^{T} \mathbf{b} = \sum_{i=1}^3 a_i b_i \]

  • The inner product of vector \(\boldsymbol{a}\) and a tensor \(\boldsymbol{T}\) produces a vector \(\boldsymbol{b}\)，is non-commutative if the tensor is non-symmetric:

    \[ \mathbf{b} = \mathbf{T} \cdot \mathbf{a} = \sum_{i=1}^3 \sum_{j=1}^3 T_{ij}a_j = \left( \begin{array}{cccc} T_{11} a_1 & + & T_{12} a_2 & + & T_{13} a_3 \\ T_{21} a_1 & + & T_{22} a_2 & + & T_{23} a_3 \\ T_{31} a_1 & + & T_{32} a_2 & + & T_{33} a_3 \end{array} \right) \]

    \[ \mathbf{b} = \mathbf{a} \cdot \mathbf{T} = \sum_{i=1}^3 \sum_{j=1}^3 a_jT_{ji} \]

    if \(\mathbf{T}\) is a symmetric tensor, that is \(\mathbf{T}_{ij} = \mathbf{T}_{ji}\), then \(\mathbf{a} \cdot \mathbf{T} = \mathbf{T} \cdot \mathbf{a}\)

• Outer product 外积

  • The outer product (dyadic product) of two vectors \(\mathbf{a}, \mathbf{b}\) is a tensor

    \[ \mathbf{T}=\mathbf{a} \otimes \mathbf{b}=\mathbf{a b}^T=\left[\begin{array}{lll} a_x b_x & a_x b_y & a_x b_z \\ a_y b_x & a_y b_y & a_y b_z \\ a_z b_x & a_z b_y & a_z b_z \end{array}\right] \]

    Usually, sign \(\otimes\) is neglected for brevity as shown below:

    \[ \mathbf{a}\mathbf{b} \]

    But the first one is mathematically correct.

• Cross product 叉乘
  • the cross product of \(\mathbf{a} \times \mathbf{b}\) is vector that perpendicular to both \(\mathbf{a}\) and \(\mathbf{b}\), which defines a plane.

  • the magnitude of the cross product of two vectors represents the area of the parallelogram spanned by the two vectors

    两向量叉乘的模为该两向量所组成的平行四边形的面积

  \[ \mathbf{a} \times \mathbf{b} = \left| \begin{array}{lll} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ a_1 & a_2 & a_3\\ b_1 & b_2 & b_3 \end{array} \right| = \left[ \begin{array}{l} a_2 b_3 - b_2 a_3 \\ a_1 b_3 - b_1 a_3 \\ a_1 b_2 - b_1 a_2 \end{array}\right] \]

• Differential Operators

  The spatial derivative of a variable (scalar, vector or tensor) is made by using the "Nabla" operator \(\nabla\) or "del". It contains the three space derivatives of \(x,y,z\) in a Cartesian coordinate system: \[ \nabla = \left(\begin{array}{l} \frac{\partial}{\partial x} \\ \frac{\partial}{\partial y} \\ \frac{\partial}{\partial z} \end{array}\right) \]

  • Gradient Operator 梯度

    • the gradient of a scalar \(\phi\) results in a vector \(\mathbf{a}\): \[ \text{grad} \phi = \nabla\phi = \left(\begin{array}{l} \frac{\partial \phi}{\partial x} \\ \frac{\partial \phi}{\partial y} \\ \frac{\partial \phi}{\partial z} \end{array}\right) \]

    • the gradient of a vector \(\mathbf{b}\) results in a tensor \(\mathbf{T}\) \[ \text{grad} \mathbf{b} = \nabla \otimes \mathbf{b} = \nabla \mathbf{b} = \left[\begin{array}{lll} \frac{\partial}{\partial x} b_x & \frac{\partial}{\partial x} b_y & \frac{\partial}{\partial x} b_z \\ \frac{\partial}{\partial y} b_x & \frac{\partial}{\partial y} b_y & \frac{\partial}{\partial y} b_z \\ \frac{\partial}{\partial z} b_x & \frac{\partial}{\partial z} b_y & \frac{\partial}{\partial z} b_z \end{array}\right] \] So the gradient operation increases the rank of the tensor by one.

  • Divergence Operator 散度
    • The divergence of a vector \(\mathbf{b}\) results in a scalar \(\phi\), and can be expressed by the Nabla and the dot sign \(\bullet\), \(\nabla \bullet\): \[ \text{div} \mathbf{b} = \nabla \bullet \mathbf{b} = \sum_{i=1}^3 \frac{\partial}{\partial x_i} \mathbf{b_i} = \frac{\partial b_1}{\partial x_1} + \frac{\partial b_2}{\partial x_2} + \frac{\partial b_3}{\partial x_3} \]
      • Physically the divergence of vector field over a region is a measure of how much the vector field points into or out of the region.
    • The divergence of a tensor \(\mathbf{T}\) results in a vector \(\mathbf{b}\): \[ \text{div} \mathbf{T} = \nabla \bullet \mathbf{T} = \frac{\partial}{\partial x_j} \mathbf{T_{ji}} = \left[\begin{array}{llll} \frac{\partial T_{11}}{\partial x_1} + \frac{\partial T_{21}}{\partial x_2} + \frac{\partial T_{31}}{\partial x_3} \\ \frac{\partial T_{12}}{\partial x_1} + \frac{\partial T_{22}}{\partial x_2} + \frac{\partial T_{32}}{\partial x_3} \\ \frac{\partial T_{13}}{\partial x_1} + \frac{\partial T_{23}}{\partial x_2} + \frac{\partial T_{33}}{\partial x_3} \end{array}\right] \]

    So the divergence operation decreases the rank of the tensor by one.

    • The product Rule within the divergence operator
      • The divergence of the product of vector \(\mathbf{a}\) and a scalar \(\phi\) \[ \nabla \bullet (\mathbf{a} \phi) = \mathbf{a} \bullet \nabla \phi + \phi \nabla \bullet \mathbf{a} \]
      • The divergence of the outer product of two vectors \(\mathbf{a}\) and \(\mathbf{b}\) \[ \nabla \bullet (\mathbf{a} \otimes \mathbf{b}) = \nabla \bullet (\mathbf{a} \mathbf{b}) = \mathbf{a} \bullet \nabla \mathbf{b} + \mathbf{b} \nabla \bullet \mathbf{a} \]
  • Other operations on the Nabla Operator
    • the divergence of the gradient of a scalar variable \(\boldsymbol{s}\) is denoted by the Laplacian of \(\boldsymbol{s}\) and is a scalar

    \[ \nabla \cdot (\nabla\boldsymbol{s}) = \nabla ^2 \boldsymbol{s} = \frac{\partial ^2 \boldsymbol{s}}{\partial x^2} + \frac{\partial ^2 \boldsymbol{s}}{\partial y^2} + \frac{\partial ^2 \boldsymbol{s}}{\partial z^2} \]